Category

Art Categories. A Note on Size Limitation for All Art Categories Affiliate Partners may limit the size of work that they accept. Please refer to your local guidelines.

Schematic representation of a category with objects X, Y, Z and morphisms f, g, g ∘ f. (The category's three identity morphisms 1 X, 1 Y and 1 Z, if explicitly represented, would appear as three arrows, from the letters X, Y, and Z to themselves, respectively.) Category theory formalizes and its concepts in terms of a labeled called a, whose nodes are called objects, and whose labelled directed edges are called arrows (or ). A has two basic properties: the ability to the arrows, and the existence of an arrow for each object. The language of category theory has been used to formalize concepts of other high-level such as,,. Informally, category theory is a general theory of. Several terms used in category theory, including the term 'morphism', are used differently from their uses in the rest of mathematics. In category theory, morphisms obey conditions specific to category theory itself.

And introduced the concepts of categories,, and in 1942–45 in their study of, with the goal of understanding the processes that preserve mathematical structure. Category theory has practical applications in, for example the usage of. It may also be used as an axiomatic foundation for mathematics, as an alternative to and other proposed foundations.

Contents • • • • • • • • • • • • • • • • • • • • • • • • Basic concepts [ ] Categories represent abstractions of other mathematical concepts. Many areas of mathematics can be formalised by category theory as. Hence category theory uses abstraction to make it possible to state and prove many intricate and subtle mathematical results in these fields in a much simpler way. A basic example of a category is the, where the objects are sets and the arrows are functions from one set to another. However, the objects of a category need not be sets, and the arrows need not be functions.

Any way of formalising a mathematical concept such that it meets the basic conditions on the behaviour of objects and arrows is a valid category—and all the results of category theory apply to it. The 'arrows' of category theory are often said to represent a process connecting two objects, or in many cases a 'structure-preserving' transformation connecting two objects.

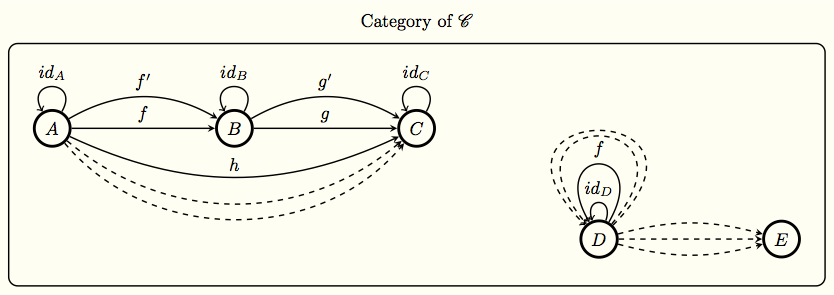
There are, however, many applications where much more abstract concepts are represented by objects and morphisms. The most important property of the arrows is that they can be 'composed', in other words, arranged in a sequence to form a new arrow. Applications of categories [ ] Categories now appear in many branches of mathematics, some areas of where they can correspond to or to, and where they can be used to describe. Probably the first application of category theory outside pure mathematics was the 'metabolism-repair' model of autonomous living organisms. Utility [ ] Categories, objects, and morphisms [ ].

This section needs additional citations for. Unsourced material may be challenged and removed. Find sources: – ( November 2015) () The study of is an attempt to axiomatically capture what is commonly found in various classes of related by relating them to the structure-preserving functions between them. A systematic study of category theory then allows us to prove general results about any of these types of mathematical structures from the axioms of a category. Radmin no tray icon.

Consider the following example. The Grp of consists of all objects having a 'group structure'. One can proceed to about groups by making logical deductions from the set of axioms defining groups.

For example, it is immediately proven from the axioms that the of a group is unique. Instead of focusing merely on the individual objects (e.g., groups) possessing a given structure, category theory emphasizes the – the structure-preserving mappings – between these objects; by studying these morphisms, one is able to learn more about the structure of the objects. In the case of groups, the morphisms are the. A group homomorphism between two groups 'preserves the group structure' in a precise sense; informally it is a 'process' taking one group to another, in a way that carries along information about the structure of the first group into the second group.

Zrazok protokolu virobnicho naradi v dnz. Host value ttl zneznama.cz 37.58.104.178 1799 host value ttl pri zneznama.cz hub2.intencio.eu 1799 0 zneznama.cz hub.intencio.cz 1799 10 host value ttl zneznama.cz ns.gransy.com 1799 zneznama.cz ns2.gransy.com 1799 zneznama.cz ns3.gransy.com 1799 zneznama.cz ns4.gransy.com 1799 zneznama.cz ns5.gransy.com 1799 host value ttl zneznama.cz Mname: ns.gransy.com Rname: root.gransy.com Serial: Refresh: 86400 Retry: 900 Expire: 1209600 Minimum-ttl: 1800 1799 host value ttl zneznama.cz Txt: v=spf1 a mx include:spf.mandrillapp.com include:_spf.intencio.cz include:_spf.mlsend.com -all 1799.